Visualizing sound signals
Representing sound with numbers
Before the digital revolution, which started in the 1960s, sound was predominantly recorded by etching the pressure waveform on a physical medium. During playback the etched waveform was tracked and converted to vibrations of a diaphragm. This is a beautiful idea, and you will be amazed to know that the quality was very good. To know more try seeing this video.
In current times, having witnessed the digital revolution, sound signals are stored as discrete sequences of numbers in physical mediums such as semiconductors. This approach is more efficient compared to vinyl records, and hence, have made the capture and playback of sound signals easily accessible. Your mobile phone does it every time you are talking on the phone. When it comes to digital capture of an analogue signal, following needs some understanding,
-
sampling frequency (fs): As the name implies, it refers to picking a few samples from a continuous-time signal (or waveform). Sampling frequency refers to the number of samples you pick per second, samples being spaced uniformly apart in time. Obviously, while you are sampling you are also discarding a lot. Is there a critical sampling frequency when the discarding is not going to hurt you? Yes, and this rate is referred to as the Nyquist-rate. It is equal to the twice the maximum frequency content in the continuous-time signal you are interested to sample. In our case this signal of interest is sound, and a good choice of fs is 48 kHz for music signals and 16 kHz for speech signals. A beautiful illustration of this is provided here and more details here
-
quantization: Once we have sampled in time, the next step is to store the amplitude values taken by the signal at the sampled time instants. These amplitude values will be stored in the computer (or more specifically, disk drives) and this storage has a finite resolution for storing a number decided by the number of bits used to represent a number. These bits can be n = 2,4,8, 16, 32, etc. For n bits, the resolution is (1/(2^n-1)). So, more the number of bits, higher is the resolution and hence, the representation (or storage) of the number in the memory of the computer will be more accurate. Sound (or audio) is usually stored at 16-bits. For more details you can read this).
Hurray, a sampled and quantized analogue signal can be stored in any digital media. And once we have stored it, we can also read (or load) it back from the digital media! In step 1, we will attempt reading (or loading) a sound file stored in the github server, and visualize (and hear) the content inside it.
Loading a sound file
We will load a file 'nMIOAh7qRFf3pqbchclOLKbPDOm1_heavy_cough.wav'. Any WAV file has some metadata stored inside it. This metadata gives information about the sampling frequency, quantization bits, number of channels, etc., used during the capture (and) storage of the sound file. Below we show a screenshot of this information for our file.
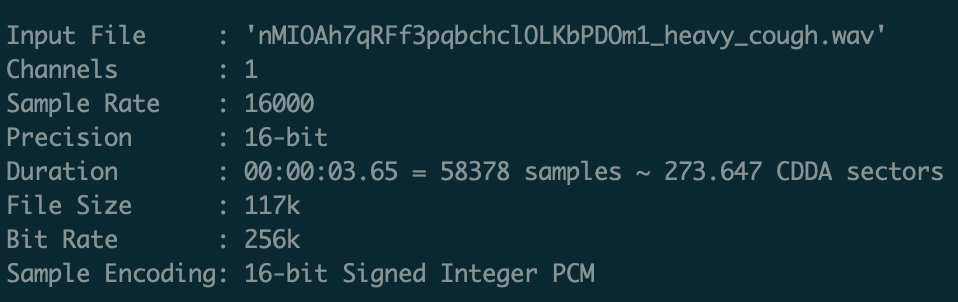
We can see that the fs is 16 kHz. Lets now load, listen, and plot the data inside this sound file.
#collapse
import numpy as np
import librosa
from IPython.lib.display import Audio
import matplotlib.pyplot as plt
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns
fs = 16000
fname = 'nMIOAh7qRFf3pqbchclOLKbPDOm1_heavy_cough.wav'
dname = './my_data/'
# load
x, sr = librosa.load(dname+fname,sr=16000)
x = x/max(np.abs(x))
times = np.arange(0,len(x))/fs
# listen
Audio(x, rate=sr, autoplay=False)
#collapse
# plot
fig = plt.subplots(figsize=(12,4))
ax = plt.subplot(1,1,1)
ax.plot(times, x)
ax.grid(True)
plt.ylabel('amplitude [in A.U.]', fontsize=14)
plt.xlabel('time [in sec]', fontsize=14)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
The signal starts with silence, and around 0.5 sec we see the start of the first cough. This is followed by two more, and then a pause which might be an inhaling of air. Subsequently. we see three more coughs. Lets visualize the distribution of the sample values.
#collapse_show
fig = plt.subplots(figsize=(12,4))
ax = plt.subplot(1,2,1)
ax.hist(x,bins=1000,range=(x.min(), x.max()))
ax.grid(True)
plt.ylabel('COUNT', fontsize=14)
plt.xlabel('amplitude [in A.U]', fontsize=14)
# plt.xticks(fontsize=13)
# plt.yticks(fontsize=13)
plt.xlim(-.1,.1)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax = plt.subplot(1,2,2)
ax.scatter(x[:-1],x[1:])
ax.grid(True)
plt.ylabel('x [n+1]', fontsize=14)
plt.xlabel('x [n]', fontsize=14)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
We see that the histogram (shown on the left) peaks around zero. This means most of the sample values are low amplitude (<.0125). We also plot a phase plot of x[n+1] vs x[n] on the right. This lies along y=x indicating a correlation between consecutive time samples. Such high correlation also implies high low frequency (relative to 8 kHz) content in the signal. We will verify this observation using Fourier transform.
Spectrum of a sound signal
A time-domain signal can be analyzed using Fourier transform. (To be fair, any signal can be analyzed using Fourier transform). Via a Fourier transform we can visualize the frequency (or spectral) content in the signal. This is useful for sound signal analysis. The obtained spectral content can help us understand certain perceived attributes of the sound (namely, timbre). Lets compute and visualize the spectrum of the above sound signal.
#collapse
def nearestpow2(n):
k=1
while n>2**k:
k = k+1
return 2**k
nfft = nearestpow2(len(x))
X = np.fft.rfft(x,nfft)
freq = np.arange(0,nfft/2+1)/nfft*fs
#collapse_show
fig = plt.subplots(figsize=(16,5))
ax = plt.subplot(1,2,1)
ax.plot(freq,np.abs(X))
ax.grid(True)
plt.ylabel('MAGNITUDE SPECTRUM [in A.U]', fontsize=14)
plt.xlabel('frequency [in Hz]', fontsize=14)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax = plt.subplot(1,2,2)
ax.plot(freq,20*np.log10(np.abs(X))-np.max(20*np.log10(np.abs(X))))
ax.grid(True)
plt.ylabel('MAGNITUDE SPECTRUM [in dB]', fontsize=14)
plt.xlabel('frequency [in Hz]', fontsize=14)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.ylim(-60,10)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
The plot on the left depicts the spectrum distributed from 0 to 8 kHz (=fs/2). We see a peak (like of a mountain) around 300 Hz, and a second peak around 1500 Hz, followed by three more peaks. Also, there is a roll-off of the spectral amplitude from lower to higher frequencies. To decrease the contrast between the too high peak and other smaller peaks we can apply a dB transformation to the spectrum amplitude. The resulting plot is shown on the right. Applying dB transform for visualizing the spectral content also makes sense from perception aspects (you might have noticed sound pressure is reported in dBs).
Spectrograms
The Fourier transform helps us understand the frequency content (spectrum) of this sound signal. This is useful. Does the ear also use a similar approach to analyze a sound signal? Scientists have dissected mammalian ears and found that the organ inside the ear (referred to as the cochlea) acts to certain extent like a mechanical Fourier analyzer. In relation do check out this video. But definitely the cochlea will not wait for the whole signal to end (like in our case 3.5 secs) and then compute the Fourier transform. We hear the sound within 10 msecs. While you are listening to a speech, you don't wait for the person to finish to understand the speech, innstead you start understanding it while the person is speaking. Thus, lets take the Fourier transform of small segments of the sound signal. But how small? You are free to choose any length.
- We will use something in between 10-30 msec and the reasoning is that if the minimum frequency in the sound signal is 50 Hz then we would have at least captured 2 cycles.
- This also relates to non-stationarity in the signal. Sound signals such as speech and music have a time-varying spectral content. Hence, it makes sense to analyze the signal in short-time segments.
Don't worry if the above is not clear to you. Below is an illustration on the same. Let's understand this. From the speech signal you take a 25 msec segment, compute its magnitude Fourier transform, and push the output into a column of an empty matrix. Then you hop in time by 10 msec, and again take a 25 msec segment from the speech signal, and repeat the same thing, that is, compute magnitude Fourier transform and push the output into the next column of the matrix. This way you move from the start to end of the signal by hopping in 10 msecs. The matrix you thus obtained is called the spectrogram. It is plotted as an image (color bar: the gradient from dark blue to white indicates high to low amplitude in the spectral content). Do you like this image? You can notice some beautiful horizontal striations. These correspond to harmonic frequencies in certain time-segments in the speech signal. Some amazing folks can read out a sentence by just staring at the spectrogram. Check out this for more details.
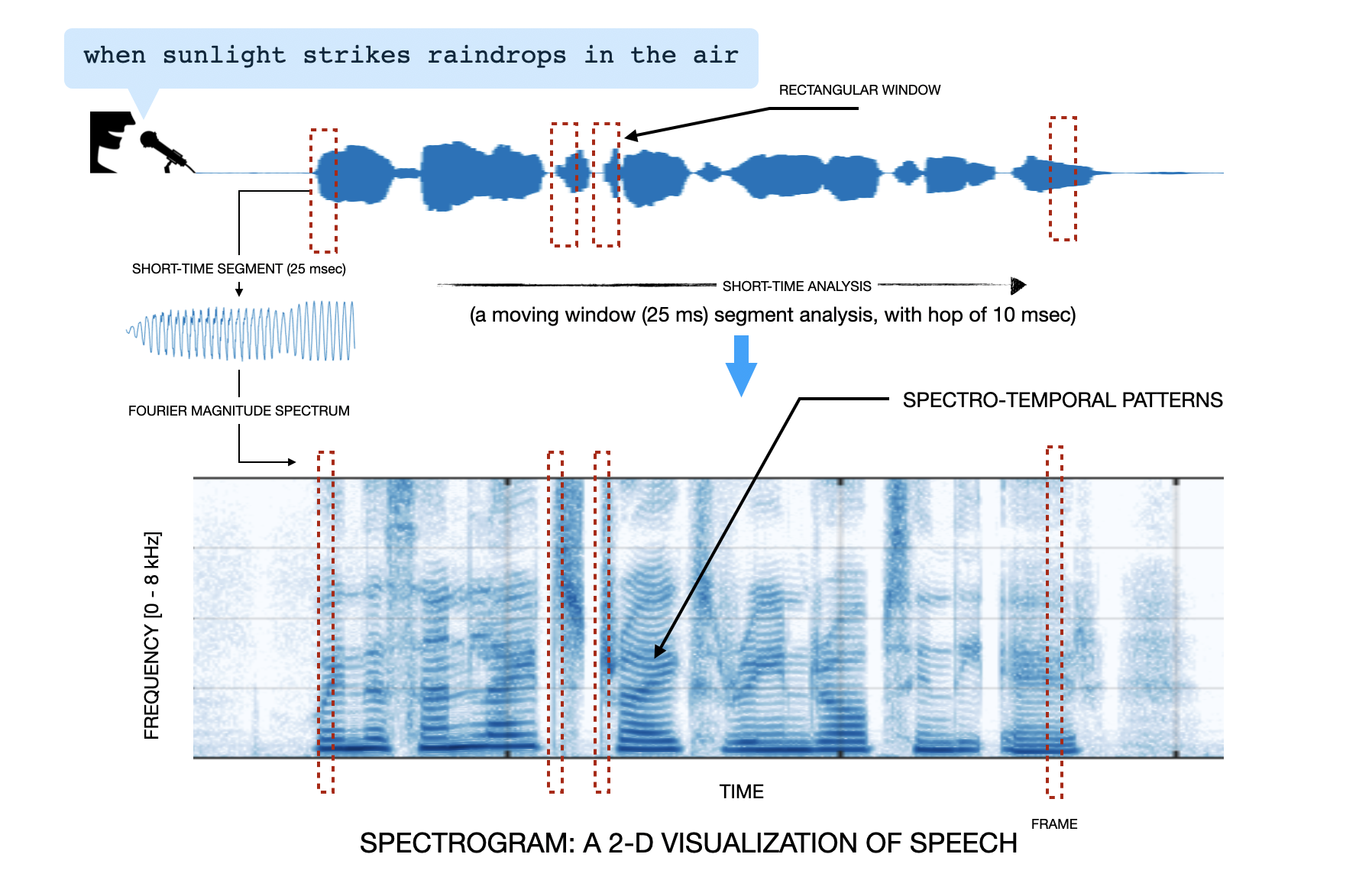
Now that we know about spectrogram, let's compute this for our cough signal.
#collapse
# first we define the spectrogram function
def generate_spectrogram(x,fs,wdur=20e-3,hdur=5e-3):
X = []
i = 0
cnt = 0
win = np.hamming(wdur*fs)
win = win - np.min(win)
win = win/np.max(win)
while i<(len(x)-int(wdur*fs)):
X.append(np.multiply(win,x[i:(i+int(wdur*fs))]))
i = i + int(hdur*fs)
cnt= cnt+1
X = np.array(X)
Xs = abs(np.fft.rfft(X))
return Xs
# lets plot now
fig = plt.subplots(figsize=(6,1))
ax = plt.subplot(1,1,1)
ax.plot(times,x)
ax.set_xlim(times[0],times[-1])
ax.set_ylim(-1,1)
ax.set_xlabel('TIME [in s]')
ax.set_ylabel('A.U')
sns.despine(offset = .1,trim=False)
plt.show()
fig, ax = plt.subplots(figsize=(6,4))
Xs = generate_spectrogram(x,fs,wdur=10e-3,hdur=2.5e-3)
XdB = 20*np.log10(Xs.T)
XdB = XdB - np.max(XdB)
im = ax.imshow(XdB,origin='lower',aspect='auto',extent = [times[0], times[-1], 0, fs/2/1e3],
cmap='RdBu_r',vmin = 0, vmax =-100)
divider = make_axes_locatable(ax)
colorbar_ax = fig.add_axes([.95, 0.1, 0.015, 0.5])
fig.colorbar(im, cax=colorbar_ax)
ax.set_xlim(times[0],times[-1])
# ax.set_xlim(.2,3)
ax.set_ylim(-.1,4)
ax.set_xlabel('TIME [in s]')
ax.set_ylabel('FREQ [in kHz]')
sns.despine(offset = 0.01,trim=False)
plt.show()